GEOMETRIA ANALÍTICA
Assinale a alternativa que expressa a transformação da equação cartesiana x+y=9 em uma equação polar.
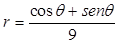
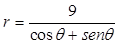
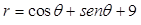
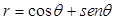
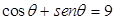
Considerando a equação da superfície expressa 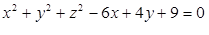 por assinale a alternativa correta.
por assinale a alternativa correta.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Assinale a alternativa que expressa um vetor de mesma direção do vetor 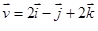 e que tenha módulo igual a metade do módulo de v.
e que tenha módulo igual a metade do módulo de v.
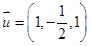

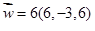
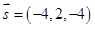
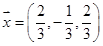
Assinale a alternativa que corresponde à equação da reta r que passa por A(-1, 2) e forma com o eixo das abscissas um ângulo de 45º, medido do eixo para a reta no sentido anti-horário.
y=-x+1
y=x-3
y=-x+3
y=x+1
y=x+3
Encontre o foco e uma equação da diretriz para a parábola y2 = -2x.
F(0, -1/2) e x = -1/2
F(0, 1/2) e x = 2
F(-2, 0) e x = 1
F(-1/2, 0) e x = 1/2
F(2, 1/2) e x = 0
O valor de m, considerando que as retas 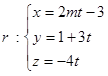 e
e 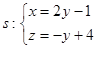 são ortogonais, está expresso na alternativa.
são ortogonais, está expresso na alternativa.
m=2
m= -1/3
m= 7/4
m=5
m= -7/4
Dados os vetores %7D) e
e %7D) . Assinale a alternativa que expressa o resultado do produto
. Assinale a alternativa que expressa o resultado do produto %7D.%7B%5Cleft(%7B%5Cvec%7B%7Bu%7D%7D%7D%2B%7B2%7D%7B%5Cvec%7B%7Bv%7D%7D%7D%5Cright)%7D) .
.
150
-205
-300
208
300
Analise as afirmativas feitas sobre a figura abaixo representada no plano cartesiano com duas dimensões, x e y, tomando-se como unidade o centímetro.
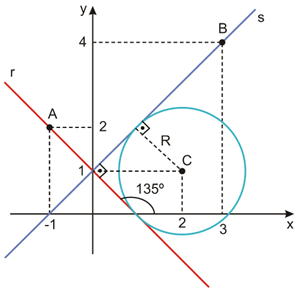
I- O raio da circunferência é  cm.
cm.
II- A equação da circunferência é (x-2)² + (y-1)² =2.
III- A equação da reta s é y=x+1.
IV- A equação da reta r é y=-x-1 .
V- A distância do ponto C(2,1) à reta r é  cm.
cm.
É correto apenas o que se afirma em
I, II e V.
II, III e IV.
I, II e III.
I, II e IV.
II, III e V.
Determine uma equação geral do plano  determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
![]()
![]()
![]()
![]()
![]()
Considerando a equação da superfície expressa 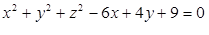 por assinale a alternativa correta.
por assinale a alternativa correta.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Assinale a alternativa que expressa um vetor de mesma direção do vetor 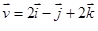 e que tenha módulo igual a metade do módulo de v.
e que tenha módulo igual a metade do módulo de v.
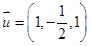

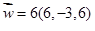
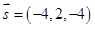
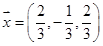
Assinale a alternativa que corresponde à equação da reta r que passa por A(-1, 2) e forma com o eixo das abscissas um ângulo de 45º, medido do eixo para a reta no sentido anti-horário.
y=-x+1
y=x-3
y=-x+3
y=x+1
y=x+3
Encontre o foco e uma equação da diretriz para a parábola y2 = -2x.
F(0, -1/2) e x = -1/2
F(0, 1/2) e x = 2
F(-2, 0) e x = 1
F(-1/2, 0) e x = 1/2
F(2, 1/2) e x = 0
O valor de m, considerando que as retas 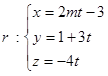 e
e 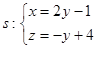 são ortogonais, está expresso na alternativa.
são ortogonais, está expresso na alternativa.
m=2
m= -1/3
m= 7/4
m=5
m= -7/4
Dados os vetores %7D) e
e %7D) . Assinale a alternativa que expressa o resultado do produto
. Assinale a alternativa que expressa o resultado do produto %7D.%7B%5Cleft(%7B%5Cvec%7B%7Bu%7D%7D%7D%2B%7B2%7D%7B%5Cvec%7B%7Bv%7D%7D%7D%5Cright)%7D) .
.
150
-205
-300
208
300
Analise as afirmativas feitas sobre a figura abaixo representada no plano cartesiano com duas dimensões, x e y, tomando-se como unidade o centímetro.

I- O raio da circunferência é  cm.
cm.
II- A equação da circunferência é (x-2)² + (y-1)² =2.
III- A equação da reta s é y=x+1.
IV- A equação da reta r é y=-x-1 .
V- A distância do ponto C(2,1) à reta r é  cm.
cm.
É correto apenas o que se afirma em
I, II e V.
II, III e IV.
I, II e III.
I, II e IV.
II, III e V.
Determine uma equação geral do plano  determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Assinale a alternativa que expressa um vetor de mesma direção do vetor 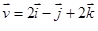 e que tenha módulo igual a metade do módulo de v.
e que tenha módulo igual a metade do módulo de v.
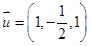

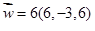
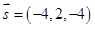
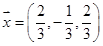
Assinale a alternativa que corresponde à equação da reta r que passa por A(-1, 2) e forma com o eixo das abscissas um ângulo de 45º, medido do eixo para a reta no sentido anti-horário.
y=-x+1
y=x-3
y=-x+3
y=x+1
y=x+3
Encontre o foco e uma equação da diretriz para a parábola y2 = -2x.
F(0, -1/2) e x = -1/2
F(0, 1/2) e x = 2
F(-2, 0) e x = 1
F(-1/2, 0) e x = 1/2
F(2, 1/2) e x = 0
O valor de m, considerando que as retas 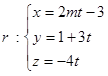 e
e 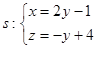 são ortogonais, está expresso na alternativa.
são ortogonais, está expresso na alternativa.
m=2
m= -1/3
m= 7/4
m=5
m= -7/4
Dados os vetores %7D) e
e %7D) . Assinale a alternativa que expressa o resultado do produto
. Assinale a alternativa que expressa o resultado do produto %7D.%7B%5Cleft(%7B%5Cvec%7B%7Bu%7D%7D%7D%2B%7B2%7D%7B%5Cvec%7B%7Bv%7D%7D%7D%5Cright)%7D) .
.
150
-205
-300
208
300
Analise as afirmativas feitas sobre a figura abaixo representada no plano cartesiano com duas dimensões, x e y, tomando-se como unidade o centímetro.

I- O raio da circunferência é  cm.
cm.
II- A equação da circunferência é (x-2)² + (y-1)² =2.
III- A equação da reta s é y=x+1.
IV- A equação da reta r é y=-x-1 .
V- A distância do ponto C(2,1) à reta r é  cm.
cm.
É correto apenas o que se afirma em
I, II e V.
II, III e IV.
I, II e III.
I, II e IV.
II, III e V.
Determine uma equação geral do plano  determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
![]()
![]()
![]()
![]()
![]()
Assinale a alternativa que corresponde à equação da reta r que passa por A(-1, 2) e forma com o eixo das abscissas um ângulo de 45º, medido do eixo para a reta no sentido anti-horário.
y=-x+1
y=x-3
y=-x+3
y=x+1
y=x+3
Encontre o foco e uma equação da diretriz para a parábola y2 = -2x.
F(0, -1/2) e x = -1/2
F(0, 1/2) e x = 2
F(-2, 0) e x = 1
F(-1/2, 0) e x = 1/2
F(2, 1/2) e x = 0
O valor de m, considerando que as retas 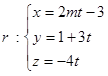 e
e 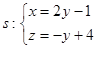 são ortogonais, está expresso na alternativa.
são ortogonais, está expresso na alternativa.
m=2
m= -1/3
m= 7/4
m=5
m= -7/4
Dados os vetores %7D) e
e %7D) . Assinale a alternativa que expressa o resultado do produto
. Assinale a alternativa que expressa o resultado do produto %7D.%7B%5Cleft(%7B%5Cvec%7B%7Bu%7D%7D%7D%2B%7B2%7D%7B%5Cvec%7B%7Bv%7D%7D%7D%5Cright)%7D) .
.
150
-205
-300
208
300
Analise as afirmativas feitas sobre a figura abaixo representada no plano cartesiano com duas dimensões, x e y, tomando-se como unidade o centímetro.

I- O raio da circunferência é  cm.
cm.
II- A equação da circunferência é (x-2)² + (y-1)² =2.
III- A equação da reta s é y=x+1.
IV- A equação da reta r é y=-x-1 .
V- A distância do ponto C(2,1) à reta r é  cm.
cm.
É correto apenas o que se afirma em
I, II e V.
II, III e IV.
I, II e III.
I, II e IV.
II, III e V.
Determine uma equação geral do plano  determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
y=-x+1
y=x-3
y=-x+3
y=x+1
y=x+3
Encontre o foco e uma equação da diretriz para a parábola y2 = -2x.
F(0, -1/2) e x = -1/2
F(0, 1/2) e x = 2
F(-2, 0) e x = 1
F(-1/2, 0) e x = 1/2
F(2, 1/2) e x = 0
O valor de m, considerando que as retas 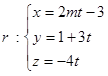 e
e 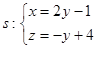 são ortogonais, está expresso na alternativa.
são ortogonais, está expresso na alternativa.
m=2
m= -1/3
m= 7/4
m=5
m= -7/4
Dados os vetores %7D) e
e %7D) . Assinale a alternativa que expressa o resultado do produto
. Assinale a alternativa que expressa o resultado do produto %7D.%7B%5Cleft(%7B%5Cvec%7B%7Bu%7D%7D%7D%2B%7B2%7D%7B%5Cvec%7B%7Bv%7D%7D%7D%5Cright)%7D) .
.
150
-205
-300
208
300
Analise as afirmativas feitas sobre a figura abaixo representada no plano cartesiano com duas dimensões, x e y, tomando-se como unidade o centímetro.

I- O raio da circunferência é  cm.
cm.
II- A equação da circunferência é (x-2)² + (y-1)² =2.
III- A equação da reta s é y=x+1.
IV- A equação da reta r é y=-x-1 .
V- A distância do ponto C(2,1) à reta r é  cm.
cm.
É correto apenas o que se afirma em
I, II e V.
II, III e IV.
I, II e III.
I, II e IV.
II, III e V.
Determine uma equação geral do plano  determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
F(0, -1/2) e x = -1/2
F(0, 1/2) e x = 2
F(-2, 0) e x = 1
F(-1/2, 0) e x = 1/2
F(2, 1/2) e x = 0
O valor de m, considerando que as retas 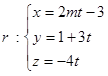 e
e 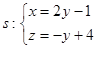 são ortogonais, está expresso na alternativa.
são ortogonais, está expresso na alternativa.
m=2
m= -1/3
m= 7/4
m=5
m= -7/4
Dados os vetores %7D) e
e %7D) . Assinale a alternativa que expressa o resultado do produto
. Assinale a alternativa que expressa o resultado do produto %7D.%7B%5Cleft(%7B%5Cvec%7B%7Bu%7D%7D%7D%2B%7B2%7D%7B%5Cvec%7B%7Bv%7D%7D%7D%5Cright)%7D) .
.
150
-205
-300
208
300
Analise as afirmativas feitas sobre a figura abaixo representada no plano cartesiano com duas dimensões, x e y, tomando-se como unidade o centímetro.

I- O raio da circunferência é  cm.
cm.
II- A equação da circunferência é (x-2)² + (y-1)² =2.
III- A equação da reta s é y=x+1.
IV- A equação da reta r é y=-x-1 .
V- A distância do ponto C(2,1) à reta r é  cm.
cm.
É correto apenas o que se afirma em
I, II e V.
II, III e IV.
I, II e III.
I, II e IV.
II, III e V.
Determine uma equação geral do plano  determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
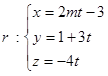 e
e 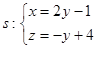 são ortogonais, está expresso na alternativa.
são ortogonais, está expresso na alternativa.m=2
m= -1/3
m= 7/4
m=5
m= -7/4
Dados os vetores %7D) e
e %7D) . Assinale a alternativa que expressa o resultado do produto
. Assinale a alternativa que expressa o resultado do produto %7D.%7B%5Cleft(%7B%5Cvec%7B%7Bu%7D%7D%7D%2B%7B2%7D%7B%5Cvec%7B%7Bv%7D%7D%7D%5Cright)%7D) .
.
150
-205
-300
208
300
Analise as afirmativas feitas sobre a figura abaixo representada no plano cartesiano com duas dimensões, x e y, tomando-se como unidade o centímetro.

I- O raio da circunferência é  cm.
cm.
II- A equação da circunferência é (x-2)² + (y-1)² =2.
III- A equação da reta s é y=x+1.
IV- A equação da reta r é y=-x-1 .
V- A distância do ponto C(2,1) à reta r é  cm.
cm.
É correto apenas o que se afirma em
I, II e V.
II, III e IV.
I, II e III.
I, II e IV.
II, III e V.
Determine uma equação geral do plano  determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
150
-205
-300
208
300
Analise as afirmativas feitas sobre a figura abaixo representada no plano cartesiano com duas dimensões, x e y, tomando-se como unidade o centímetro.

I- O raio da circunferência é  cm.
cm.
II- A equação da circunferência é (x-2)² + (y-1)² =2.
III- A equação da reta s é y=x+1.
IV- A equação da reta r é y=-x-1 .
V- A distância do ponto C(2,1) à reta r é  cm.
cm.
É correto apenas o que se afirma em
I, II e V.
II, III e IV.
I, II e III.
I, II e IV.
II, III e V.
Determine uma equação geral do plano  determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.
determinado pelos pontos de coordenadas A(0,0,0), B(1,1,5) e C(-1, 1,1) e assinale a alternativa correta.

I, II e V.
II, III e IV.
I, II e III.
I, II e IV.
II, III e V.